画像フィルター

フィルターとは、大きなものと小さなものをよりわけるフルイのこと である。大きなものは周波数でいうと小さな周波数を持ち、小さなもの は大きな周波数を持っているので、入力画像をフーリエ変換して、 適当な重み関数を掛けてやればよいことになる。

ところが、スペクトル空間での掛け算は実空間での畳み込み積分 (convolution)に相当するので、実空間のみでの計算が可能である。

ここで、g は畳み込み関数と呼ばれていて、G のフーリエ逆変換で 求めます。

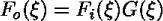
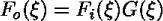
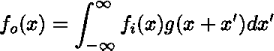
畳み込み積分は、走行平均(running average)を考えると理解しやすい でしょう。走行平均はデータの平均を計算する窓をずらしながら平均値を 求めていくことでおおまかな傾向をつかもうとするものです。

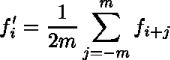
さて、この計算を２次元のデータ構造を持つ画像データに適用する わけですが、この計算を行うツールとして、pnmconvolという コマンドがあります。man pnmconvolを読むとわかります が、このコマンドの使用にはかなり注意が必要です。

まず最初に、畳み込み関数の設計をします。この関数は PGM ファイル に作成します。 PGM ファイルのデータは正の整数値しかとれませんので、 PGM ファイルフォーマットで定義される最大値の半分の値を 0 と解釈 するようになっています。また、最大値の半分で正規化されるので、平均計算 に必要な割り算はあらかじめデータに入っていなくてはなりません。

以下の 3 x 3 の領域を平均化する例を見てください。

         P2
         3 3
         18
         10 10 10
         10 10 10
         10 10 10
この例では、最大値が18ですから、最大値の半分の 9 が 0 に相当します。 ですから、データ値 10 は、1 に相当します。また、正規化に使われる 数も 9 ですから、それぞれのデータ値は 1/9 の重みをもっていることに なります。もし、5x5 の平均をしたければ、最大値は 5x5x2 = 50、データ 値としては、25+1 の 26 を使えばよいことがわかります。

コマンドの実行は、低域通過フィルターの畳み込み関数ファイルを lpf.pgm としたとき、 

        % pnmconvol lpf.pgm johoto.pgm > joho-lpf.pgm
のようにします。 5x5 の単純走行平均をかけた例を以下の画像に示します。

上の例は低域通過フィルターですが、元の画像から、低域通過フィルターを 通した画像を差し引けば高域通過フィルターができます。5x5の広域通過フィルターの 例です。(右の表はオフセットを除いた整数値です) 
        P2
        5 5
        50
        24 24 24 24 24    -1 -1 -1 -1 -1
        24 24 24 24 24    -1 -1 -1 -1 -1
        24 24 49 24 24    -1 -1 24 -1 -1
        24 24 24 24 24    -1 -1 -1 -1 -1
        24 24 24 24 24    -1 -1 -1 -1 -1
この例では畳み込み積分の実行で負の計算結果は 0 に丸められてしまうことに 注意してください。以下の結果の画像は、結果を見やすくするために ガンマ値を 10 にして補正してあります。

フィルターには今までのような上下左右に対称なものだけでなく、 非対称のものもあります。例えば 
        P2
        3 3
        2
        1 2 1            0  1  0
        0 1 2           -1  0  1
        1 0 1            0 -1  0
のようなフィルターを使うと、これは右上から左下方向への微分を表す ことになります。このフィルターを適用した結果は以下のとおりです。

このような非対称フィルターはエッジの検出に使われることがあります。 よく使われるもののひとつに Sobel のオペレータと呼ばれるものがあります。 x 方向、y方向のエッジの検出に、それぞれ以下のようなフィルターが 用いられます。 
          -1  0  1         -1 -2 -1
       X: -2  0  2      Y:  0  0  0
          -1  0  1          1  2  1
結果は以下のようになります。それぞれ x,y 方向の線をとらえている ことがわかると思います。

実際のエッジ検出には逆方向の微分も必要です。pnmconvol だけを使って この計算を行うのは煩雑になります。pgmedge というコマンドは x y 方向の Sobel のオペレータを使ってその2乗和を出力します。 以下が実行例です。