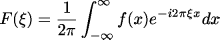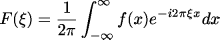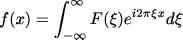フーリエ変換

信号を波長の異なる波に分解する。

1次元のフーリエ変換

時間的に変化する信号(例:音、地震動、温度)を周波数毎の成分に分解する。

距離の関数として変化しているもの(例:水路にできた波)を空間波数成分に分解する。

2次元のフーリエ変換

距離と時間の関数として変化しているもの(例:水路にできた進行する波、電磁波、光) を空間波数と周波数の成分に分解する。

平面上の信号の強弱分布(例:画像)を空間波数成分に分解する。

フーリエ係数(フーリエ変換)の性質

ゆっくりした変化は

波数が小さい

小さいものは

波数空間での広がりが大きい

１次元のフーリエ変換

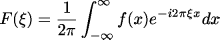
１次元のフーリエ逆変換

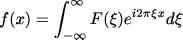
２次元フーリエ変換

• 原画像
• 実数(cos)成分
• 虚数(sin)成分

高速フーリエ変換 FFT