7人でマージャンを
次のような問題を考えてみましょう。
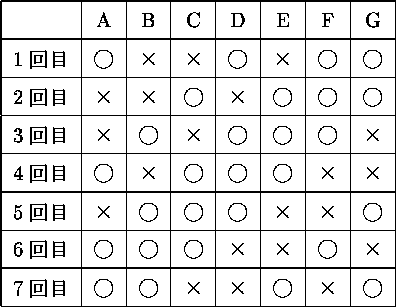
『 7人でマージャンを7回やり
(a) どの人も4回ずつ参加し、
(b) どの2人も2回ずつ顔が合う
ように組み合わせを定めよ 』
そのひとつの解は、7人のメンバーをAさん、Bさん、・・・、Gさんとし、

で与えられます。 この組み合わせは勿論試行錯誤によっても見つけることができますが、 『 有限射影幾何学 』と呼ばれる数学の知識を用いればすぐに見つけることができます。
今日はこの『 有限射影幾何学 』という考え方を、 幾何学とは、射影幾何学とは、有限幾何学とは、 といった順番で説明してゆき、 その情報科学への応用について述べます。
では先ず、中学校の頃に習った平面のユークリッド幾何学の復習をしましょう。
平面のユークリッド幾何学
平面の上では、点・直線・線分・線分の長さ・角度という概念が定義され、
これらを元にして、ピタゴラスの定理、図形の合同問題、
作図問題等々が展開されていました。
ユークリッド幾何学は「平行線の公理」と呼ばれる命題
『 直線 l と、l 上にない1点 P が与えられたとき、 P を通り l に平行な直線が唯1本存在する 』
を正しいものとして構築されています。ピタゴラスの定理や
『 三角形の内角の和は 180° である 』といった命題は実はこの公理から導かれます。
それでは「平行線の公理」を仮定しないで幾何学ができないでしょうか。
球面の幾何学
私達は「真直な道」という言い方をしますが、
道は地球の表面を走っているのですから、
「真直な道」をどんどん伸ばしてゆけば地球を一周して
円になってしまいます。
(ここでは地球は完全な球だと思ってください。)
その円は赤道や子午線の様に球面上に描くことのできる一番大きな
円なので「大円」と呼ばれます。
この考え方を活かして
『 球面上の“直線” = 大円 』と定義することにより、球面上で幾何学を展開することができます。 それは「平行線の公理」の成り立たない幾何学であり、例えば
『 三角形の内角の和は常に 180° より大きい 』という定理が成り立ちます。
射影平面の幾何学(非ユークリッド幾何学)
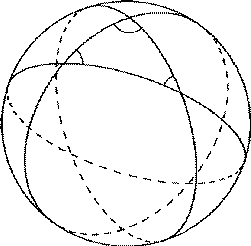
球面上のふたつの大円は、北極と南極の様に球の中心に関して対称な2点で
交わります。このため、球面幾何学では
『 異なる2点を通る“直線”は1本には定まらない 』という奇妙な事が起こります。
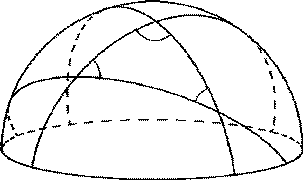
そこで北半球だけを考え ( 正確には赤道も半分だけ北半球に入れます )、
『 北半球上の“直線” = 大円のうち北半球に含まれる部分 』と定義すると、 「平行線の公理」から導かれる定理を除けば 平面のユークリッド幾何学とほとんど同様の幾何学 ( 非ユークリッド幾何学と言います ) が構築できます。
【注意】「北半球だけを考える」ということは、言い換えれば
『 球の中心に関して対称な2点は同じものだと思う 』ということです。 その意味で上に述べた幾何学を「射影幾何学」、 北半球のことを「射影平面」と呼びます。 また
射影平面の“直線”= 原点を通る平面と北半球の交わり
であることにも注意しておきましょう。
有限幾何学
ふたつの数0と1のみから成る集合 F={0,1} に足し算と掛け算を次の表で
定義しましょう。

すると F は実数全体の集合と同じく「加減乗除」の定義された集合となります。
通常の幾何学は実数を座標に持つ図形を扱いますが、 その座標を F の元0と1に限っても幾何学を展開することが可能です。 座標に使える数が有限個しかないという意味でこれを『 有限幾何学 』と呼びます。 ( F 以外にも色々な集合を座標に用いることができます。) 今の場合、 有限射影平面は原点以外の3次元の点から成る集合
S={(1,0,0),(0,1,0),(0,0,1),(1,1,0),(1,0,1),(0,1,1),(1,1,1)}
であり、
S の“直線”= 原点を通る平面から原点を除いた集合となっています。
ブロックデザイン
有限射影平面 S には7本の“直線”があります。
l = {(0,0,1),(0,1,0),(0,1,1)} =「平面 x=0 から原点を除いた集合」,
1
l = {(1,0,0),(0,0,1),(1,0,1)} = 「平面 y=0 から原点を除いた集合」,
2
l = {(1,0,0),(0,1,0),(1,1,0)} = 「平面 z=0 から原点を除いた集合」,
3
l = {(0,0,1),(1,1,1),(1,1,0)} = 「平面 x+y=0 から原点を除いた集合」,
4
l = {(1,0,0),(0,1,1),(1,1,1)} = 「平面 y+z=0 から原点を除いた集合」,
5
l = {(1,0,1),(0,1,1),(1,1,0)} = 「平面 x+y+z=0 から原点を除いた集合」,
6
l = {(0,1,0),(1,0,1),(1,1,1)} = 「平面 x+z=0 から原点を除いた集合」.
7
幾何学的な意味を考えれば、この7本の“直線”は
(1)各“直線”は3つの点をもっている (2)Sの点を2つ与えると、その2点を含む“直線”が唯1本存在するという性質をもっていることが分かります。 この性質は一般に『 ブロックデザイン 』と呼ばれるもののひとつで、 部分集合の間の、或る「非常に良い対称性」と言えます。 S の 7つの点にそれぞれ A(1,0,0), B(0,0,1), C(0,1,0), D(1,0,1), E(0,1,1), F(1,1,1), G(1,1,0) と名前を付け、 各点が“直線”li 上にあるとき ×、 そうでないとき 〇 を書いた表を作れば、 今日最初にお話したマージャンの対戦表が得られることに気付くでしょう。
誤り訂正符号
今日、様々な情報が通信によってやり取りされています。
しかし通信には雑音が付き物ですから、
情報を必要最小限だけ送信していたのでは
受信者はしょっちゅう誤った情報を受け取ることになります。
そこで『 誤り訂正符号 』というものが考え出されました。
情報はディジタル通信では0と1の信号(ビットと呼びます) の組み合わせによって表現されます。 このとき、情報自体の信号(情報ビット)の他に 「検査ビット」と呼ばれる“おまけ”を付けると、 その“おまけ”の効果によって、通信中に生じた誤りを 受信者が訂正することが可能になります。 “おまけ”の付け方には様々なテクニックがあり、 今日お話しした有限射影幾何学もそのひとつです。